Qu’est-ce qu’un CAPTCHA par preuve de travail (PoW)?
Un CAPTCHA par preuve de travail (PoW CAPTCHA) empêche les abus automatisés et le spam en demandant à l’appareil de l’utilisateur d’effectuer un calcul en arrière-plan.
Limites des défis PoW classiques
Certains appareils résolvent le défi en quelques secondes, d’autres mettent un temps infini — ou abandonnent. Ces temps de résolution imprévisibles nuisent à l’expérience utilisateur.
Comment Friendly Captcha a révolutionné la preuve de travail
Plutôt que de proposer un seul défi difficile, Friendly Captcha en propose plusieurs, plus simples. Cela réduit fortement la variance des temps de résolution.
Pionnier des CAPTCHA nouvelle génération basés sur la PoW
Friendly Captcha a repensé le modèle de preuve de travail pour les CAPTCHA : meilleure UX, moins d’abandons et fiabilité accrue.
Essayer maintenant ›
Les algorithmes Proof of work (PoW ou preuve de travail) n’ont généralement aucune notion de progrès, ils reviennent plutôt à jouer des millions de fois à la loterie jusqu’à finir par gagner. Perdre un million de fois n’a aucune incidence sur vos chances de gagner la fois suivante.
Nous avons créé un captcha open source, bien plus convivial et basé sur le proof of work. L’important est que le calcul nécessaire à ce captcha soit sensiblement le même pour tous les utilisateurs et, plus encore, qu’il n’y ait aucune valeur aberrante.
Dans l’exemple de la loterie, il n’y a aucune garantie, un utilisateur peut très bien gagner du premier coup tandis qu’un autre aura besoin de nombreuses tentatives. Avant d’entrer dans les détails et de parler de cette solution simple, revenons sur les propriétés d’un bon problème proof of work.
Notre configuration proof of work
L’idée derrière le PoW est que la vérification du puzzle (ou tâche) soit peu coûteuse, mais son calcul bien plus coûteux.
Un PoW consistant à « hacher cette chaîne 1 million de fois » serait coûteux à calculer, mais tout aussi coûteux à vérifier. Au lieu de cela, la plupart des algorithmes PoW demandent à l’utilisateur de chercher une aiguille dans une botte de foin : on génère une chaîne de puzzles pet l’on demande à l’utilisateur de trouver un nonce q de sorte que le hachage de p et de q concaténés réponde à certains critères rares. Si l’on utilise une bonne fonction de hachage, n’importe quelle chaîne d’entrée a autant de probabilités de répondre à ce critère qu’une autre.
Rappelez-vous que tout octet ou chaîne peut être interprété comme un nombre. On prend les 4 premiers octets du hachage et on les interprète comme un nombre entier de 32 bits. Si ce nombre est inférieur à un certain seuil T (que l’on pourrait désigner comme l’inverse de la difficulté), il s’agit alors d’une solution valable. Toute entrée de hachage a la même probabilité de satisfaire ce critère, de sorte que pour trouver la solution, l’utilisateur doit simplement essayer différentes valeurs pour le nonce q jusqu’à tomber sur une solution gagnante. Ce n’est donc pas si différent que de jouer beaucoup à la loterie !
Vérification dans pseudocode
puzzleString = "my-puzzle-string"
threshold = 1000 // Plus la valeur est basse, plus l'énigme est difficile à résoudre
nonce = "3456356782345" // C'est la valeur que le solveur modifie pour essayer de trouver une solution valide.
hash_result = hash(puzzleString + nonce)
value = toUint32(hash_result[0:4])
si valeur < seuil {
print "Valide !"
} else {
print "Solution non valide :("
}Combien de tentatives cela prend-il ?
Si vos chances de gagner à la loterie sont d’une sur un million, au bout d’un million de tentatives, vos chances de gagner au moins une fois sont d’environ 63,2% (1 - (1/one_million)^one_million ou 1 - binom.pmf(1, one_million, 1/one_million)). Voici un graphique de densité :
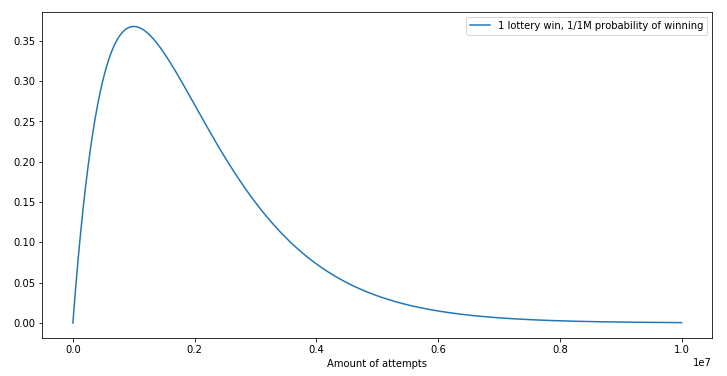
La plupart des gens y parviendront en un million de tentatives, toutefois certains utilisateurs vraiment malchanceux auront besoin de 3 millions d’essais (~5% en fait), voire davantage ! Autrement dit, le nombre de tentatives nécessaires varie considérablement. Ceci pose problème dans le cas d’une PoW de CAPTCHA : les utilisateurs renoncent forcément lorsque l’opération prend 5 fois plus de temps que prévu. Peu leur importe la moyenne mathématique, ils veulent juste pouvoir s’inscrire sur votre site web.
Pour que l’expérience utilisateur soit correcte, il faut également que l’utilisateur puisse se fier à une sorte d’indicateur de progression. Se contenter d’afficher « résolution du captcha en cours »pendant 10 secondes sans la moindre indication fera renoncer l’utilisateur qui va s’imaginer que le site web ne fonctionne pas. Si, au lieu de cela, on lui propose une barre de progression qui se remplit avec le temps, il va se montrer bien plus compréhensif.
Le problème est qu’il n’y a pas de progression en soi, personne ne peut savoir quand il va trouver le nonce créant un hachage apte à remplir les critères. Il existe heureusement une solution directe au problème de la progression et de la variance : nous demandons aux utilisateurs de trouver plus d’un nonce.
Problèmes multiples et plus faciles
Au lieu d’obliger l’utilisateur à trouver le nonce 1 sur 1 million, nous pouvons l’obliger à trouver 10 nonces pour un problème 1 sur 100k. Le nombre de tentatives attendues est toujours le même, mais nous pouvons maintenant montrer une barre de progression à l’utilisateur !
On résout ainsi le problème de la progression d’une part, tout en réduisant également la variance du nombre total de tentatives requises. La variance baisse à mesure que l’on augmente le nombre de nonces demandés. Voyons ce que cela donne de façon graphique :
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import binom
un_million = 1000000
n_attempts = np.arange(0, 5*one_million, 1000)
fraction_still_solving_1m = [binom.cdf(1, n, 1/one_million) for n in n_attempts]
fraction_still_solving_500k = [binom.cdf(2, n, 2/one_million) for n in n_attempts]
fraction_still_solving_200k = [binom.cdf(5, n, 5/one_million) for n in n_attempts]
fraction_still_solving_100k = [binom.cdf(10, n, 10/one_million) for n in n_attempts]
fraction_still_solving_50k = [binom.cdf(20, n, 20/one_million) for n in n_attempts]
plt.figure(figsize=(12, 6))
plt.plot(n_attempts, fraction_still_solving_1m, label="1 gain de loterie, 1/1M")
plt.plot(n_attempts, fraction_still_solving_500k, label="2 lottery wins, 1/500K")
plt.plot(n_attempts, fraction_still_solving_200k, label="5 lottery wins, 1/200K")
plt.plot(n_attempts, fraction_still_solving_100k, label="10 lottery wins, 1/100K")
plt.plot(n_attempts, fraction_still_solving_50k, label="20 lottery wins, 1/50K")
plt.legend()
plt.ylabel("Fraction qui n'a pas encore fini")
plt.xlabel("Nombre de tentatives")
plt.show()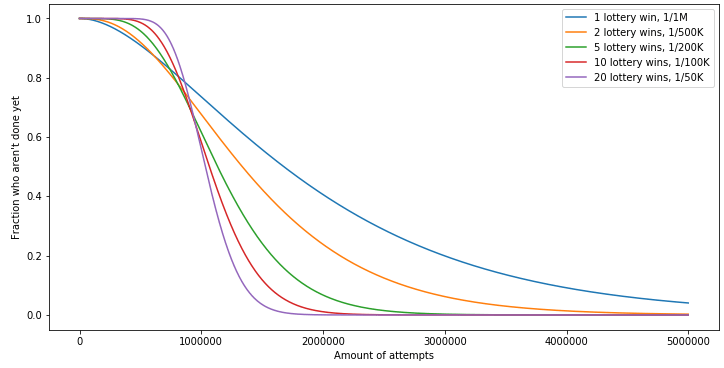
Ce graphique montre que si l’on demande aux gens de jouer à une seule loterie, 1 personne sur 10 environ mettra plus de 4 fois plus de temps que la moyenne ! Une telle statistique est inacceptable pour un CAPTCHA, mais à mesure que l’on augmente le nombre de gains requis pour une loterie plus simple, l’on diminue considérablement la variance. Sous forme de tableau, voilà combien de personnes n’auraient pas encore terminé au bout de N tentatives :
| Nombre de solutions nécessaires | 1M tentatives | 2M tentatives | 3M tentatives |
|---|---|---|---|
| 1 | un sur 1.4 | un sur 2.5 | un sur 2.5 |
| 2 | un sur 1.5 | un sur 4.2 | un sur 16 |
| 5 | un sur 1.6 | un sur 14.9 | un sur 358 |
| 10 | un sur 1.7 | un sur 92.5 | un sur 45K |
| 20 | un sur 1.8 | un sur 2715 | un sur 512M |
Il est également possible de représenter la fonction de masse de probabilité (ci-dessous) sur un graphique, fonction qui montre clairement la variance. Le nombre attendu de tentatives est peu ou prou le même, mais la variance est bien plus faible.

Les inconvénients de la multiplication des solutions
Solliciter davantage de solutions n’est pas sans inconvénient, à commencer par la nécessité de soumettre plus de solutions, ce qui se traduit par des besoins accrus en bande passante. Dans Friendly Captcha, chaque solution est une valeur de 8 octets transmise en base64. Passer de 10 à 20 solutions nécessiterait donc environ 106 caractères supplémentaires (10*8*(4/3)).
Deuxièmement, il y a tout simplement plus de solutions à vérifier, toutefois la vérification étant peu coûteuse, ce point est sans importance.
Conclusion
Le proof of work ne comporte généralement pas de notion de progression. Chacune des tentatives a autant de chances que celle qui la suit de trouver la solution. En demandant plusieurs solutions de proof of work, nous pouvons réduire la variance et fournir une notion de progression, deux caractéristiques qui sont des exigences pour un CAPTCHA basé sur le proof of work.
Envie de voir le CAPTCHA proof of work à l’œuvre? Essayez la démo ici. La bibliothèque captcha open source et le code du widget sont disponibles ici.
FAQ
Un service CAPTCHA de preuve de travail comme Friendly Captcha demande aux robots de résoudre un petit puzzle cryptographique avant d’accéder à une fonctionnalité du site web. Pour les vrais utilisateurs, le défi est résolu automatiquement et de manière invisible en arrière-plan. La technique de preuve de travail augmente le coût des attaques automatisées, offrant une protection robuste contre les robots sans suivi ni interaction avec l’utilisateur.
Le CAPTCHA de preuve de travail augmente la protection contre les robots en exigeant la résolution d’une petite énigme cryptographique à l’aide de ressources informatiques. Bien que les humains ne soient pas affectés, ce mécanisme ralentit les robots et rend les attaques automatisées à grande échelle impossibles.
Le meilleur CAPTCHA de preuve de travail est Friendly Captcha. Pour une sécurité maximale, il combine des mécanismes de preuve de travail avec une mise à l’échelle avancée des risques pour éliminer les attaques de robots et une protection avancée contre le spam.