Was ist ein Proof-of-Work CAPTCHA?
Ein Proof-of-Work CAPTCHA (PoW CAPTCHA) soll automatisierten Missbrauch und Spam verhindern, indem das Gerät des Nutzers im Hintergrund eine Rechenaufgabe lösen muss.
Limitationen bei den traditionellen Proof-of-Work Aufgaben
Manche Geräte lösen die PoW-Aufgabe in Sekunden, andere brauchen ewig – oder brechen ab. Diese unvorhersehbaren Zeiten sorgen für eine schlechte Nutzererfahrung.
Wie Friendly Captcha das Proof-of-Work-Prinzip revolutioniert
Anstatt dem Gerät eine schwere Aufgabe zu geben, stellt Friendly Captcha mehrere leichtere PoW-Aufgaben. So wird die Varianz der Lösungszeiten deutlich reduziert.
Pionier der nächsten Generation von PoW-CAPTCHAs
Friendly Captcha hat das Proof-of-Work-Prinzip für CAPTCHAs neu gedacht – für eine bessere User Experience, weniger Abbrüche und eine höhere Sicherheit. Jetzt starten ›
PoW-Algorithmen (Proof of Work) haben im Allgemeinen keine Vorstellung von Fortschritt, sondern sind eher so, als würden Sie Millionen von Malen Lotto spielen, bis Sie gewinnen. Wenn Sie eine Million Mal verlieren, hat das keinen Einfluss auf Ihre Gewinnchancen beim nächsten Mal.
Wir haben ein benutzerfreundlicheres Open Source Captcha entwickelt, das auf Proof of Work basiert. Es ist wichtig, dass dieses Captcha für jeden Benutzer ungefähr den gleichen Rechenaufwand erfordert, und noch wichtiger, dass es keine Ausreißer gibt.
Im Beispiel der Lotterie gibt es keine Garantien, ein Benutzer könnte beim ersten Versuch gewinnen, ein anderer braucht vielleicht viele Versuche. Bevor wir uns mit den Einzelheiten und der einfachen Lösung befassen, sollten wir die Eigenschaften eines guten Proof-of-Work-Problems untersuchen.
Unser Proof-of-Work-Setup
Die Idee hinter PoW ist, dass das Rätsel (auch als Herausforderung) muss billig zu verifizieren, aber teuer zu berechnen sein.
Ein PoW, der “diese Zeichenkette 1 Million Mal hashen” würde, wäre teuer in der Berechnung, aber ebenso teuer in der Verifizierung. Stattdessen lassen die meisten PoW-Algorithmen den Benutzer nach einer Nadel im Heuhaufen suchen: Wir generieren eine Rätselkette pund bitten Sie den Benutzer, eine nonce q so dass der Hash von p und q konkateniert wird, einige seltene Kriterien erfüllt. Wenn wir eine gute Hash-Funktion verwenden, ist es genauso wahrscheinlich, dass eine beliebige Eingabezeichenkette dieses Kriterium erfüllt wie eine andere.
Denken Sie daran, dass jedes Byte oder jeder String als Zahl interpretiert werden kann. Wir nehmen die ersten 4 Bytes des Hashes und interpretieren sie als 32-Bit-Ganzzahl. Wenn diese Zahl unter einem bestimmten Schwellenwert T liegt (den Sie als den Kehrwert der Schwierigkeit bezeichnen könnten), handelt es sich um eine gültige Lösung. Jede Hash-Eingabe erfüllt dieses Kriterium mit gleicher Wahrscheinlichkeit. Um die Lösung zu finden, würde der Benutzer also einfach verschiedene Werte für die Nonce ausprobieren q bis sie eine gewinnbringende Lösung finden. Das ist nicht viel anders als ein Lotteriespiel!
Verifizierung in Pseudocode
puzzleString = "mein-puzzle-string"
threshold = 1000 // Je niedriger, desto schwieriger ist das Rätsel
nonce = "3456356782345" // Dies ist der Wert, den der Löser ändert, um eine gültige Lösung zu finden
hash_result = hash(puzzleString + nonce)
Wert = toUint32(hash_result[0:4])
wenn Wert < Schwellenwert {
print "Gültig!"
} else {
print "Ungültige Lösung :("
}Wie viele Versuche sind nötig?
Wenn Ihre Chancen, im Lotto zu gewinnen, eins zu einer Million stehen, beträgt Ihre Chance, nach einer Million Versuchen mindestens einmal zu gewinnen, etwa 63,2% (1 - (1/one_million)^one_million oder 1 - binom.pmf(1, one_million, 1/one_million)). Hier ist ein Dichteplot:
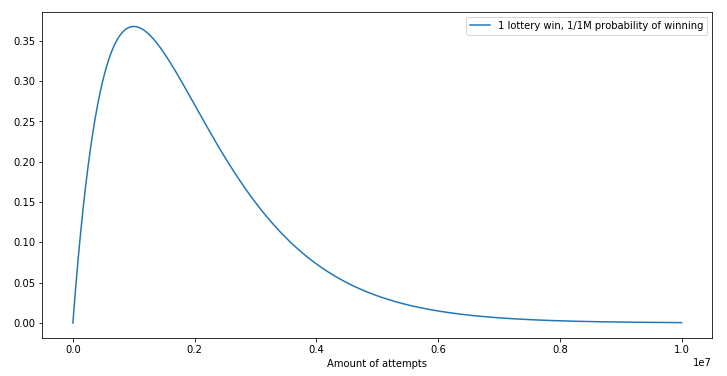
Die meisten Menschen benötigen etwa eine Million Versuche, aber einige Benutzer haben wirklich Pech und benötigen stattdessen 3 Millionen Versuche (~5% in der Tat) oder sogar mehr! Mit anderen Worten: Es gibt eine große Varianz bei der Anzahl der benötigten Versuche. Das ist problematisch für ein PoW CAPTCHA: Der Benutzer wird das Warten aufgeben, wenn es 5 Mal länger dauert als erwartet. Es ist ihm egal, was der mathematische Durchschnitt ist, er möchte sich einfach nur auf Ihrer Website anmelden.
Für ein angemessenes Benutzererlebnis verdient der Benutzer auch eine Art Fortschrittsanzeige. Einfach nur anzeigen “das Captcha lösen” Wenn Sie 10 Sekunden lang keine Anzeige sehen, wird der Benutzer aufgeben und denken, die Website sei defekt. Wenn es stattdessen einen Fortschrittsbalken gibt, der mit der Zeit ansteigt, ist das viel erträglicher.
Das Problem ist, dass es keinen Fortschritt gibt. Niemand weiß, wann er die Nonce finden wird, die einen Hash erzeugt, der die Kriterien erfüllt. Glücklicherweise gibt es eine einfache Lösung sowohl für das Problem des Fortschritts als auch der Varianz: Wir bitten die Benutzer, mehr als eine Nonce zu finden.
Mehrere, einfachere Probleme
Anstatt den Benutzer dazu zu bringen, die 1:1 Million Nonce zu finden, können wir ihn 10 Nonces für ein 1:100k Problem finden lassen. Die erwartete Anzahl von Versuchen ist immer noch die gleiche, aber jetzt können wir dem Benutzer einen Fortschrittsbalken zeigen!
Wir lösen nicht nur das Fortschrittsproblem, sondern verringern auch die Varianz, wie viele Versuche insgesamt erforderlich waren. Wenn wir die Anzahl der Nonces erhöhen, die wir abfragen, nimmt die Varianz ab. Lassen Sie uns das grafisch darstellen:
import matplotlib.pyplot as plt import numpy as np from scipy.stats import binom eine_million = 1000000 n_versuche = np.arange(0, 5*eine_million, 1000) fraction_still_solving_1m = [binom.cdf(1, n, 1/one_million) for n in n_attempts] fraction_still_solving_500k = [binom.cdf(2, n, 2/one_million) for n in n_attempts] fraction_still_solving_200k = [binom.cdf(5, n, 5/one_million) for n in n_attempts] fraction_still_solving_100k = [binom.cdf(10, n, 10/one_million) for n in n_attempts] fraction_still_solving_50k = [binom.cdf(20, n, 20/one_million) for n in n_attempts] plt.figure(figsize=(12, 6)) plt.plot(n_attempts, fraction_still_solving_1m, label="1 Lottogewinn, 1/1M") plt.plot(n_attempts, fraction_still_solving_500k, label="2 Lottogewinne, 1/500K") plt.plot(n_attempts, fraction_still_solving_200k, label="5 Lottogewinne, 1/200K") plt.plot(n_attempts, fraction_still_solving_100k, label="10 Lottogewinne, 1/100K") plt.plot(n_attempts, fraction_still_solving_50k, label="20 Lottogewinne, 1/50K") plt.legend() plt.ylabel("Anteil derer, die noch nicht fertig sind") plt.xlabel("Anzahl der Versuche") plt.show()
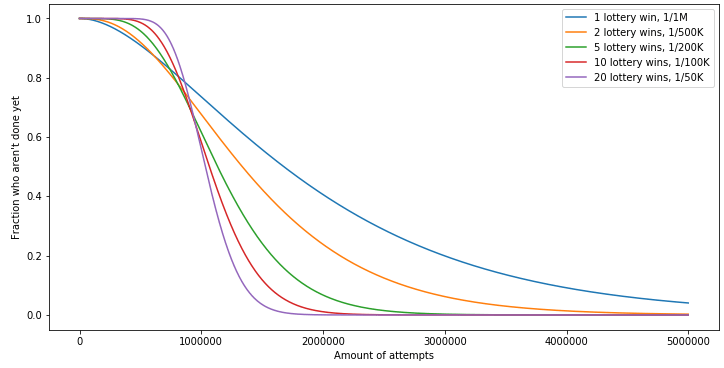
Wenn wir uns diese Grafik ansehen, sehen wir, dass etwa 1 von 10 Personen mehr als viermal so lange braucht wie der Durchschnitt, wenn wir sie eine einzige Lotterie spielen lassen! Das ist für ein CAPTCHA inakzeptabel, aber wenn wir die Anzahl der erforderlichen Gewinne für eine einfachere Lotterie erhöhen, verringert sich die Varianz erheblich. In Tabellenform, wie viele Personen nach N Versuchen noch nicht fertig sind:
| Menge der benötigten Lösungen | 1M Versuche | 2M Versuche | 3M Versuche |
|---|---|---|---|
| 1 | eins zu 1.4 | eins zu 2.5 | eins zu 2.5 |
| 2 | eins zu 1.5 | eins zu 4.2 | eins zu 16 |
| 5 | eins zu 1.6 | eins zu 14.9 | eins zu 358 |
| 10 | eins zu 1.7 | eins zu 92.5 | eins zu 45K |
| 20 | eins zu 1.8 | eins zu 2715 | eins zu 512M |
Wir können auch die Wahrscheinlichkeitsmassenfunktion (unten) aufzeichnen, die die Varianz ebenfalls deutlich zeigt. Die erwartete Anzahl der Versuche ist ungefähr gleich, aber die Varianz ist viel geringer.

Die Nachteile der Forderung nach mehr Lösungen
Es gibt einige Nachteile, wenn mehr Lösungen benötigt werden. Der erste ist die Notwendigkeit, mehr Lösungen zu übermitteln, was ein wenig mehr Bandbreite erfordert. Bei Friendly Captcha ist jede Lösung ein 8-Byte-Wert, der als base64 übertragen wird. Wenn Sie also von 10 auf 20 Lösungen erhöhen, benötigen Sie etwa 106 zusätzliche Zeichen (10*8*(4/3)).
Zweitens gibt es einfach mehr Lösungen zu verifizieren, aber da die Verifizierung billig ist, spielt das keine Rolle.
Fazit
Bei Proof-of-Work gibt es in der Regel keine Vorstellung von Fortschritt. Jeder Versuch ist genauso wahrscheinlich wie der nächste, die Lösung zu finden. Indem wir mehrere Lösungen für den Proof-of-Work verlangen, können wir die Varianz verringern und eine Vorstellung vom Fortschritt vermitteln. Beides sind Voraussetzungen für ein CAPTCHA, das auf Proof-of-Work basiert.
Möchten Sie das Proof of Work CAPTCHA in Aktion sehen? Probieren Sie die Demo hier. Die Open-Source-CAPTCHA-Bibliothek und den Widget-Code finden Sie hier.
FAQ
Ein Proof-of-Work-CAPTCHA-Service wie Friendly Captcha erfordert, dass Bots ein kleines kryptografisches Rätsel lösen, bevor sie Zugriff auf eine Website-Funktion erhalten. Für echte Menschen wird die Aufgabe automatisch und unsichtbar im Hintergrund gelöst. Die Proof-of-Work-Technik erhöht die Kosten automatisierter Angriffe und bietet einen robusten Bot-Schutz ohne Nachverfolgung oder Benutzerinteraktion.
Ein Proof-of-Work-CAPTCHA erhöht den Bot-Schutz, indem ein kleines kryptografisches Rätsel mithilfe von Rechenressourcen gelöst werden muss. Während Menschen nicht betroffen sind, verlangsamt dieser Mechanismus Bots und macht groß angelegte automatisierte Angriffe praktisch unmöglich.
Das beste Proof-of-Work-CAPTCHA ist Friendly Captcha. Für maximale Sicherheit kombiniert es Proof-of-Work-Mechanismen mit fortschrittlicher Risikoskalierung, um Bot-Angriffe zu eliminieren, und bietet einen fortschrittlichen Spam-Schutz.